Приложения к нормализации
Теорема Хита
Важное свойство (приводящее к немедленному применению) функциональных зависимостей состоит в том, что если R является отношением со столбцами, названными из некоторого набора атрибутов U, и R удовлетворяет некоторой функциональной зависимости X → Y, тогда где Z = U — XY. Интуитивно, если функциональная зависимость X → Y сохраняется в R , то отношение можно безопасно разделить на два отношения рядом со столбцом X (который является ключевым для ), гарантируя, что при обратном соединении двух частей данные не будут потеряны, т
Е. Функциональная зависимость обеспечивает простой способ построения декомпозиции соединения R без потерь на два меньших отношения. Этот факт иногда называют теоремой Хитса ; это один из первых результатов теории баз данных.
R=ΠXY(R)⋈ΠXZ(R){\displaystyle R=\Pi _{XY}(R)\bowtie \Pi _{XZ}(R)}ΠXY(R)⋈ΠXZ(R){\displaystyle \Pi _{XY}(R)\bowtie \Pi _{XZ}(R)}
Теорема Хита фактически говорит, что мы можем извлечь значения Y из большого отношения R и сохранить их в одно, которое не имеет повторений значений в строке для X и фактически является таблицей поиска для Y с ключом X и, следовательно, имеет только одно место для обновления Y, соответствующего каждому X, в отличие от «большого» отношения R, где существует потенциально много копий каждого X , каждая со своей копией Y, которую необходимо синхронизировать при обновлениях. (Это устранение избыточности является преимуществом в контекстах OLTP , где ожидается много изменений, но не так много в контекстах OLAP , которые в основном связаны с запросами.) Декомпозиция Хита оставляет только X, чтобы действовать как внешний ключ в оставшейся части большой таблицы. .
ΠXY(R){\displaystyle \Pi _{XY}(R)}ΠXZ(R){\displaystyle \Pi _{XZ}(R)}
Однако функциональные зависимости не следует путать с зависимостями включения , которые являются формализмом для внешних ключей; Несмотря на то, что они используются для нормализации, функциональные зависимости выражают ограничения по одному отношению (схеме), тогда как зависимости включения выражают ограничения между схемами отношений в схеме базы данных . Более того, эти два понятия даже не пересекаются при классификации зависимостей : функциональные зависимости — это зависимости, порождающие равенство, тогда как зависимости включения — это зависимости, порождающие кортежи . Применение ссылочных ограничений после декомпозиции схемы отношений (нормализации) требует нового формализма, то есть зависимостей включения. В разложении, полученном в результате теоремы Хита, нет ничего, препятствующего вставке кортежей, в которых некоторое значение X не найдено .
ΠXZ(R){\displaystyle \Pi _{XZ}(R)}ΠXY(R){\displaystyle \Pi _{XY}(R)}
Нормальные формы
Нормальные формы — это уровни нормализации базы данных, которые определяют «качество» таблицы. Обычно третья нормальная форма считается «хорошим» стандартом для реляционной базы данных.
Нормализация направлена на освобождение базы данных от аномалий обновления, вставки и удаления. Это также гарантирует, что когда новое значение вводится в отношение, оно оказывает минимальное влияние на базу данных и, следовательно, минимальное влияние на приложения, использующие базу данных.
Нормализация базы данных
Нормализация базы данных – это рекомендации по проектированию.
Преимущества нормализованной базы данных:
- Возможность существенно упростить выборки. Получение данных из базы относительно простыми запросами.
- Целостность данных. Избежание потерь или искажения информации в базе данных.
- Отсутствие избыточности. Данные в таблице не дублируются, что существенно снижает её размер.
- Благоприятные предпосылки к росту базы.
Как привести базу данных к нормальной форме?
Для приведения базы к нормальной форме необходимо выполнить следующие действия:
- Постараться объединить данные в группы.
- Найти логические связи между этими группами данных. Для установки связей связываемые поля должны быть одного типа и таблица формата InnoDB.
Существует 3 нормальные формы базы данных:
-
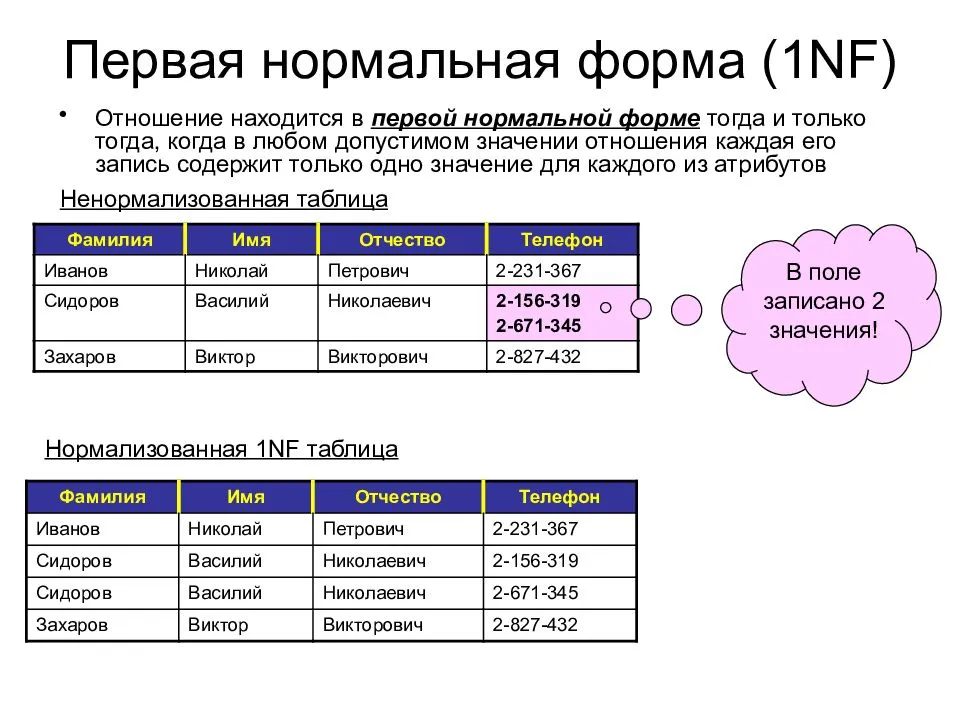
Первая нормальная форма
Таблица представляет сущность которая в ней размещена (например клиенты, заказы и т.д.) Причём в каждой таблице имеется уникальное поле (первичный ключ) например id и каждая таблица состоит из наименьшего количества полей.
Пример №1:id name languages 1 Иван Java, C++, PHP 2 Пётр PHP, JavaScript 3 Михаил C#, JavaScript В примере №1. Представлена не удачная структура таблицы, где в поле languages указано перечисление.
Пример №2:id name languages1 languages2 languages3 1 Иван Java C++ PHP 2 Пётр PHP JavaScript NULL 3 Михаил C# JavaScript NULL
В примере №2 тоже не верная структура таблицы для поля languages.
Правильная структура таблиц для решения данной задачи:
Пример №3:
Таблица пользователей
id name languages 1 Иван Java, C++, PHP 2 Пётр PHP, JavaScript 3 Михаил C#, JavaScript Таблица языков программирования
id language 1 Java 2 PHP 3 C# 4 JavaScript 5 Java Таблица связей между пользователями и языками программирования
id language_id user_id 1 2 1 2 1 1 3 5 1 4 1 2 -
Вторая нормальная форма
Для второй нормальной формы требуется первая нормальная форма.Пример №4:
id make model 1 bmw X5 2 bmw X6 3 audi A4 4 audi Q5 5 toyota corolla В примере №4 мы видим дублирование некоторых марок автомобилей (Данные избыточны). Требуется сделать разделение на несколько таблиц как в примере №3. На первый взгляд создание новых таблиц кажется более затратным чем реализация в примере №4, но это только до тех пор когда таблица состоит всего из нескольких строк.
Правильная структура таблиц для решения данной задачи: -
Третья нормальная форма
Требуется вторая нормальная форма.
Согласно третьей нормальной форме данные не должны храниться в таблице, которые могут быть получены из не ключевых полей.Пример №5:
Таблица цен и цен с НДС
id price price_nds 1 1100 1243 2 950 1074 Так как цену с НДС можно получить из поля price, то данную задачу нужно переложить на язык программирования.
Нарушения правил нормализации
Убедившись, что база данных в 3НФ поможет гарантировать надежность и жизнеспособность, не нужно полностью нормализовывать все базу, с которыми вы работаете. Перед тем, как использовать эти методы, имейте ввиду, что это может иметь долгосрочные разрушающие последствия.
Две основных причины, чтобы нарушить правила нормализации — удобство и быстродействие. Меньшим число таблиц проще управлять, чем большим. Кроме того, из-за более сложного характера, нормализованные таблицы более медленные для обновления, изменения и выдачи данных. Вкратце, нормализация это сделка между целостностью/расширяемостью и простотой/скоростью. С другой стороны, есть достаточно способов чтобы улучшить производительность базы данных, но не так много способов чтобы исправить поврежденные данные, возникшие из-за плохого дизайна структуры.
Практика и опыт подскажут, как сделать модель базы данных, но лучше совершайте ошибки пробуя нормальные формы, хотя бы до тех пор, пока не поймете принцип.
Логическое (даталогическое) проектирование
- Логическое проектирование
- создание схемы базы данных на основе конкретной модели данных, например, реляционной модели данных. Для реляционной модели данных даталогическая модель — набор схем отношений, обычно с указанием первичных ключей, а также «связей» между отношениями, представляющих собой внешние ключи.
На этапе логического проектирования учитывается специфика конкретной модели данных, но может не учитываться специфика конкретной СУБД.
Переход от ER-диаграмм к ФЗ
ER-диаграммы вполне естественным образом могут быть преобразованы к ФЗ.
Каждая сущность подразумевает ФЗ неключевых атрибутов от ключевых, поскольку значения ключевых атрибутов однозначно определяют значения остальных – иначе, значения неключевых атрибутов есть (вообще говоря, дискретная) функция от значений ключевых атрибутов.
Связи двух сущностей типа один-к-одному устанавливают взаимно-однозначное соответствие между сущностями, то есть взаимные ФЗ между ключами сущностей. Атрибуты самой связи функционально зависят от всех ключей входящих в связь сущностей.
Связи двух сущностей типа один-ко-многим и многие-к-одному естественным образом моделируют функциональную зависимость между ключевыми атрибутами соответствующих сущностей: в левой части ФЗ находятся ключевые атрибуты сущности, входящей в связь многократно, а в правой – ключевые атрибуты сущности, входящей в связь однократно, а так же атрибуты самой связи (если есть). Можно сказать, что ФЗ моделирует связь типа многие-к-одному.
Это же рассуждение естественным образом обобщается на многозначные связи: каждая из однократно входящих в связь сущностей (точнее, ее ключи) функционально зависят от всех многократно входящих в связь сущностей. То же самое можно сказать об атрибутах самой связи.
Наконец, связь типа многие-ко-многим можно рассматривать как частный случай многозначной связи: все атрибуты связи функционально зависят от всех ключевых атрибутов связанных сущностей.
Таким образом:
- Каждая сущность \(E\) преобразуется к ФЗ вида \ где \(K_E\) – множество ключевых (идентифицирующих) атрибутов сущности \(E\), а \(A_E\) – множество всех атрибутов сущности \(E\).
- Каждая связь \(R\) между сущностями \(E_1,\ldots,E_n\), входящими в связь многократно и \(S_1,\ldots,S_m\), входящими в связь однократно, преобразуется к ФЗ вида \ где \(K_i\) – ключи соответствующих сущностей, \(A_R\) – атрибуты связи, и ФЗ вида \.
Следует сделать одно важное замечание: если связь многие-ко-многим (возможно многозначная) не имеет атрибутов, то она даст исключительно тривиальные функциональные зависимости. Это, как правило, нежелательно, поскольку при формальном анализе в итоге приведет к потере этой связи
Это связано с тем, что связь многие-ко-многим является нефункциональной зависимостью. Решением этой проблемы может быть ввод фиктивного атрибута с пустым доменом, скажем, \(\theta\), уникального для данной связи. Это позволит формально анализировать функциональные зависимости для – фактически – неопределенной функции.
Диаграммы атрибутов
Кроме непосредственной записи ФЗ в столбик, существует более наглядный способ представления ФЗ отношений. Он так же может использоваться для нормализации отношения по крайней мере до 3НФ.
Диаграммы атрибутов строятся следующим образом. В овалах записываются все атрибуты данной предметной области, и между ними рисуются стрелки, соответствующие ФЗ, присутствующим в системе. В случае наличия составных левых частей ФЗ, вводятся промежуточные узлы, обозначаемые точкой.
Например, построим диаграмму атрибутов для нашего примера с теннисными кортами.
Использование диаграмм атрибутов позволяет достаточно просто обнаруживать транзитивные зависимости и выделять отдельные отношения методом простой группировки связанных узлов (атрибутов).
В качестве примера, выделим на этой диаграмме отношения. Сначала выделим все возможные ключевые атрибуты по следующему признаку: если какой-либо атрибут функционально зависит от данного, то данный атрибут является ключевым.
Теперь для каждого ключевого атрибута выделим его и все атрибуты, непосредственно зависящие от него, в отдельную группу.
Это позволит нам выделить группы атрибутов, не имеющие транзитивных зависимостей, в которых все неключевые атрибуты зависят от потенциального ключа.
Двойной линией обозначены внешние ключи.
Несложно заметить, что каждая из выделенных групп является отношением в 3НФ.
Перед началом…
Перед тем, как мы начнем изучать правила нормализации и применять их, мы должны разобраться со следующими понятиями.
Избыточность
Одним из основных моментов, который нужно учитывать при проектировании таблиц — уменьшение пространства для хранения данных. Таблицы должны быть спроектированы таким образом, чтобы повторяющиеся данные хранились отдельно, в одной или нескольких таблицах. Хранение повторяющихся данных не только требует больше места, но также приводит к более серьезным проблемам.
Таблица с данными о сотрудниках из разных отделов, содержит избыточные данные
Обратите внимание, что данные в полях DNAME и DNO неоднократно повторяются в таблице. Такой вид избыточности данных приводит к аномалиям обновления, вставки и удаления
Аномалии вставки
Если нам понадобится добавить в таблицу информацию о новом сотруднике, который не «привязан» к какому-либо отделу, данные об отделе в добавляемой записи окажутся пустыми, а это явно неоправданная трата пространства. Кроме того, при вставке данных нового сотрудника, скажем, в отдел с идентификатором ‘4’, другие поля, относящиеся к отделу, также должны будут повториться. Пример: отдел 4, поле DNAME должно содержать значение ‘Administrator’, а поле MGR_SSN — содержимое должно быть равно ‘234567890’.
Аномалии обновления
Если мы изменим значение какого-либо поля, относящегося к отделу, например, DNAME или MGR_SSN, мы должны будем изменить это значение у записей всех сотрудников, которые работают в этом отделе. Иначе, база данных будет находиться в несогласованном состоянии.
Аномалии удаления
Предположим, мы удалим информацию об одном сотруднике, например, последнюю запись из представленной выше таблицы. Только у этой записи значение в поле DNO равно ‘1’, в результате этого действия получится, что информация об отделе будет потеряна. Это нелепо, потому что мы хотим удалить информацию о сотруднике, а не обо всем отделе.
Функциональные зависимости
Функциональные зависимости — основа нормализации баз данных. Под функциональной зависимостью подразумевается зависимость значения одного поля (столбца) от другого. Например, по значению поля SSN определенного работника, мы сможем найти его адрес. Это значит, что поле адрес функционально зависимо от поля SSN. Символическая запись этой зависимости выглядит так:
{SSN} → {ADDRESS}
Аналогично,
{SSN} → {ENAME, ADDRESS} {SSN, DNO} → {MGR_SSN}
Когда значение одного или нескольких полей точно идентифицируют запись, значение такого поля называется «первичным ключом».
Связь между таблицами «один ко многим»
Связь «один ко многим» — единственно возможная в рамках требований третьей нормальной формы. В этом типе связей у строки таблицы А может быть несколько совпадающих строк таблицы Б, но каждой строке таблицы Б может соответствовать только одна строка из таблицы А. С логической точки зрения возможны два случая:
Случай первый:
Таблица А – это справочник; Таблица Б – это таблица фактов. Внешний неуникальный ключ из таблицы Б ссылается на первичный ключ таблицы А.
Случай второй:
Таблица А – это главная таблица; Таблица Б – это зависимая таблица. Внешний не уникальный ключ из таблицы Б ссылается на первичный ключ таблицы А.
Однако с физической точки зрения выглядит это одинаково: Несколько строк из таблицы Б ссылаются на одну строку таблицу А. К тому же внешний ключ таблицы Б не может быть null.
Это главное правило определяющее направление внешней связи.
Закрытие функциональной зависимости
Замыкание — это, по сути, полный набор значений, который может быть определен из набора известных значений для данного отношения, используя его функциональные зависимости. Один использует Аксиомы Армстронга предоставить доказательство — т.е. рефлексивность, увеличение, транзитивность.
Данный р{ displaystyle R} и F{ displaystyle F} набор FD, который удерживается в р{ displaystyle R}: Закрытие F{ displaystyle F} в р{ displaystyle R} (обозначен F{ displaystyle F}+) — это множество всех ФД, которые логически вытекают из F{ displaystyle F}.
Замыкание набора атрибутов
Замыкание набора атрибутов X относительно F{ displaystyle F} множество X+ всех атрибутов, которые функционально определяются X с помощью F{ displaystyle F}+.
Пример
Представьте себе следующий список ФД. Мы собираемся вычислить замыкание для A из этого отношения.
1. А → B 2. B → C3. AB → D
Закрытие будет следующим:
а) A → A (по рефлексивности Армстронга) б) A → AB (по 1. и (а)) c) A → ABD (согласно (b), 3 и транзитивности Армстронга) г) A → ABCD (согласно (c) и 2)
Следовательно, замыкание A → ABCD. Вычислив закрытие A, мы подтвердили, что A также является хорошим кандидатом ключа, поскольку его закрытие — это каждое отдельное значение данных в отношении.
Неприводимая функция в зависимости от набора
Набор функциональных зависимостей S является неприводимым, если он обладает следующими тремя свойствами:
- Каждый правый набор функциональной зависимости S содержит только один атрибут.
- Каждый левый набор функциональной зависимости S неприводим. Это означает, что уменьшение любого одного атрибута из левого набора изменит содержимое S (S потеряет некоторую информацию).
- Уменьшение любой функциональной зависимости изменит содержимое S.
Наборы функциональных зависимостей с этими свойствами также называются канонический или минимальный. Нахождение такого набора функциональных зависимостей S, который эквивалентен некоторому входному набору S ‘, предоставленному в качестве входных данных, называется поиском минимальное покрытие of S ‘: эта задача может быть решена за полиномиальное время.
Свойства и аксиоматизация функциональных зависимостей [ править ]
Учитывая, что X , Y и Z являются наборами атрибутов в отношении R , можно вывести несколько свойств функциональных зависимостей. К числу наиболее важных относятся следующие, обычно называемые аксиомами Армстронга :
- Рефлексивность : если Y является подмножеством X , то X → Y
- Увеличение : если X → Y , то XZ → YZ
- Транзитивность : если X → Y и Y → Z , то X → Z
«Рефлексивность» может быть ослаблена до справедливой , то есть это фактическая аксиома , где два других являются собственными правилами вывода , точнее порождающими следующие правила синтаксического следствия: Икс→∅{\ displaystyle X \ rightarrow \ varnothing}
⊢Икс→∅{\ displaystyle \ vdash X \ rightarrow \ varnothing}Икс→Y⊢ИксZ→YZ{\ Displaystyle X \ rightarrow Y \ vdash XZ \ rightarrow YZ}Икс→Y,Y→Z⊢Икс→Z{\ Displaystyle X \ rightarrow Y, Y \ rightarrow Z \ vdash X \ rightarrow Z}.
Эти три правила представляют собой здравую и полную аксиоматизацию функциональных зависимостей. Эта аксиоматизация иногда описывается как конечная, потому что количество правил вывода конечно, с оговоркой, что аксиома и правила вывода являются схемами , что означает, что X , Y и Z варьируются по всем основным терминам (наборам атрибутов). .
Применяя увеличение и транзитивность, можно вывести два дополнительных правила:
- Псевдотранзитивность : если X → Y и YW → Z , то XW → Z
- Состав : Если X → Y и Z → W , то XZ → YW
Также можно вывести правила объединения и разложения из аксиом Армстронга:
- X → Y и X → Z тогда и только тогда, когда X → YZ
Нормальная форма элементарного ключа (НФЭК)
НФЭК предложена Карло Занионо в 1982 году в качестве “компромисса” между 3НФ и НФБК.
- Элементарная ФЗ
- Функциональная зависимость \(f \in G\), \(f = X\to A\) называется элементарной, если она нетривиальна и замыкание \(G^+\) не содержит ФЗ \(X’\to A\) такого, что \(X’ \subset X\).
- Элементарный ключ
- Суперключ \(X\) отношения \(R\) называется элементарным ключом, если \(R\) удовлетворяет элементарной ФЗ \(X\to A\), где \(A\) – некий атрибут \(R\).
Отношение находится в НФЭК, если
- Оно находится в 3НФ
- Любая его элементарная ФЗ имеет в левой части суперключ или в правой части находится подмножество какого-либо элементарного ключа.
Иначе, отношение находится в НФЭК, если для любой его ФЗ \(X\to A\) выполняется хотя бы одно из условий:
- \(A\subset X\)
- \(X\) является суперключом.
- A входит в состав элементарного ключа
Декомпозиция без потерь
Как было сказано ранее, получить более высокую нормальную форму можно при помощи декомпозиции отношений.
- Декомпозиция
- Составление проекций \(S\), \(T\) исходного отношения \(R\), таких, что объединение заголовков \(S\) и \(T\) совпадает с заголовком \(R\).
Однако, не всякая декомпозиция допустима.
Выделяют два типа декомпозиции, используемой для нормализации.
- Декомпозиция без потерь
- Такая декомпозиция \(R\) в \((S,T)\), что \(R = S\bowtie T\).
Декомпозиция без потерь (lossless-join) позволяет восстановить исходное отношение при помощи операции соединения.
Как выбрать декомпозиции без потерь из всех возможных? Ответ на этот вопрос дает теорема Хита.
- Теорема Хита
- Пусть дано отношение \(R(A,B,C)\). Если \(R\) удовлетворяет функциональной зависимости \(A\to B\) , то \(R = \pi_{A,B} R \bowtie \pi_{A,C} R\).
Декомпозиция без потерь, однако, может не сохранять функциональные зависимости.
Например, пусть дано отношение \(R(A,B,C)\), удовлетворяющее ФЗ \(F_R=\{(A,B)\to C,C\to A\}\). По теореме Хита, \(C\to A \Rightarrow R=S(B,C)\bowtie T(C,A)\). Тогда ФЗ отношения \(S\) \(F_S=\{B\to B, C\to C\}^+\), и ФЗ отношения \(T\) \(F_T=\{C\to A\}^+\). Но \(((A,B)→C)\notin (F_S\cup F_T)^+\), и в результате оказывается потеряна.
Всегда существует декомпозиция без потерь до НФБК.
- Декомпозиция, сохраняющая зависимости
- Такая декомпозиция \(R\) в \((S,T)\), что замыкание множества ФЗ отношения \(R\) совпадает с замыканием объединения ФЗ отношений \(S\) и \(T\).
Декомпозиция, сохраняющая зависимости (dependency-preserving) сохраняет неизменным замыкание ФЗ всех отношений БД.
Всегда существует декомпозиция до НФЭК, сохраняющая зависимости. Однако, не всегда возможна декомпозиция, сохраняющая зависимости, до НФБК.
Проецирование функциональных зависимостей
Декомпозиция отношений по сути осуществляется при помощи операции проекции. При этом, мы утверждаем, что функциональные зависимости при декомпозиции сохраняются. Возникает вопрос: каким образом функциональные зависимости ведут себя при проецировании отношений?
Предположим, что имеется исходное отношение \(R\) с множеством ФЗ \(F\), и пусть \(S\) – некая проекция отношения \(R\): \ где A – некое множество атрибутов.
Тогда, множество \(G\) ФЗ, которые останутся в \(S\), это ФЗ, которые:
- Следуют из \(F\)
- Включают только атрибуты, принадлежащие \(A\)
Вполне вероятно, что множество всех ФЗ такого рода избыточно (не минимально). Сложность алгоритма поиска ФЗ отношения \(S\) в худшем случае экспоненциально зависит от количества атрибутов в \(A\).
Для нахождения всех ФЗ можно применять замыкание атрибутов из \(A\) по \(F\). Следует сделать два достаточно очевидных замечания:
- Замыкания пустого множества и множества всех атрибутов не приводят к получению нетривиальных ФЗ
- Если \(A \subset X^+\), то построение замыканий для надмножеств \(X\) не даст новых нетривиальных ФЗ в силу правила дополнения.
Так же понятно, что для любого замыкания \(X^+\), существуют ФЗ вида \(X \to B\), где \(B \subset X^+\).
Таким образом, мы можем начать с построения замыканий для единичных множеств атрибутов, и добавить все следующие из них ФЗ к множеству ФЗ \(G\), если они содержат только атрибуты из \(A\), а затем, при необходимости, построить замыкания для множеств атрибутов большей размерности.
Пример:
Пусть отношение \(R(A,B,C,D)\) имеет следующие ФЗ:
- \(A \to B\)
- \(B \to C\)
- \(C \to D\)
Пусть теперь мы получаем проекцию \(S = \pi_{A,C,D} R\). Найдем ФЗ \(G\) отношения \(S\).
Для этого, построим замыкания для всех атрибутов отношения \(S\) по \(F\). Поскольку \(B\) не входит в отношение \(S\), его замыкание не даст нам ФЗ, входящих в \(G\). \ \ \
Можем заметить, что \({A,C,D} \subset {A}^+\), соответственно, рассмотрение надмножеств \({A}\) не имеет смысла. Следовательно, единственное неединичное множество атрибутов, требующее рассмотрения это \
Запишем множество нетривиальных ФЗ \(S\), получающиеся из этих замыканий: \ \ \
Теперь найдем минимальное множество ФЗ. По правилу транзитивности, ФЗ \(A \to D\) следует из двух других, поэтому его можно исключить. В итоге, получаем минимальное множество ФЗ \(S\): \ \